46 years of history
Introduction
 Math Kangaroo was proposed by Peter O'Halloran, an Australian mathematician and teacher, in the 1980's. In 1991, this idea was taken up in Paris, France. Very quickly, it spread throughout Europe. The competition began to be called "Kangaroo" because of its Australian origin. The main purpose of Math Kangaroo is to promote mathematical thinking and stimulate an interest in math, by providing students with an opportunity to compare their abilities worldwide.
Math Kangaroo was proposed by Peter O'Halloran, an Australian mathematician and teacher, in the 1980's. In 1991, this idea was taken up in Paris, France. Very quickly, it spread throughout Europe. The competition began to be called "Kangaroo" because of its Australian origin. The main purpose of Math Kangaroo is to promote mathematical thinking and stimulate an interest in math, by providing students with an opportunity to compare their abilities worldwide.
Math Kangaroo is now the largest math competition for school students in the world. As of now, it has been held in 109 countries and regions. In 2025, approximately 6.5 million students participated globally.
In 2024, initiated by 17 countries and regions, the Kangaroo Global Committee launched the "Math Kangaroo Tournament" worldwide.
This initiative aims to provide a diverse and enjoyable approach to learning mathematics, encouraging students to connect through math and solve problems collaboratively. Through teamwork, students will ignite their passion for mathematics and experience its true charm.
To promote the elites' communication, deepen the dissemination of the "Association Kangourou sans Frontières", and aim to nurture future mathematicians, Math Kangaroo hosts the International Camps globally every summer, inviting participants who achieve gold award.
Being selected to the Math Kangaroo Camp will be a very rare international honour and a very exciting maths learning experience to the participants. The content modules of Math Kangaroo International Camps across continents are generally consistent, with slight adjustments based on the mathematical resources of the host country.
MK Advancement System
Around 6.5 million students in the world participate in "Math Kangaroo" in 2025

United States
53,562
Mexico
34,406
Honduras
19,879
Costa Rica
7,578
Canada
6,875
Dominican Republic
5,295
Jamaica
4,680
Puerto Rico
2,216

Brazil
1,502,507
Peru
36,442
Colombia
35,027
Venezuela
18,071
Argentina
14,708
Bolivia
11,988
Chile
5,443
Paraguay
3,351

Ecuador
1,970
Panama
1,594
Uruguay
521
Germany
881,500
Czech Republic
420,653
France
311,700
Poland
304,635
Russia
248,920

Catalonia
148,672
Austria
127,169
Belgium
121,315
Netherlands
109,878
Sweden
101,402
Belarus
87,058
Slovakia
75,982
Portugal
72,522

Slovenia
70,281
Italy
66,925
Ukraine
62,384
Switzerland
62,157
Bulgaria
58,019
Hungary
36,563
Croatia
34,494
Lithuania
31,358

Spain
26,589
Estonia
22,916
Romania
20,933
Finland
20,922
Norway
15,315
United Kingdom
13,320
Denmark
13,221
Latvia
12,891

Serbia
11,429
Moldova
9,190
North Macedonia
7,472
Bosnia and Herzegovina
5,191
Montenegro
3,288
Kosovo
2,015
Albania
1,399
Ireland
799

Morocco
85,882
Egypt
25,650
Ghana
8,493
South Africa
7,435
Cameroon
3,318
Uganda
2,913
Botswana
1,587
Rwanda
1,576

Nigeria
1,176
Kenya
600
Mauritania
420
Zambia
340
Tunisia
201
Mali
172
Indonesia
143,720
Kazakhstan
111,689

India
80,404
Malaysia
76,949
Mauritania
420
Pakistan
46,192
Saudi Arabia
42,109
Philippines
35,398
Vietnam
27,843
Israel
17,481

Mongolia
14,289
Uzbekistan
13,557
Kyrgyzstan
11,720
South Korea
11,050
Iran
11,023
Afghanistan
9,896
Thailand
6,230
Singapore
6,106

Palestine
5,161
Myanmar
3,977
Lebanon
3,200
Qatar
3,164
Armenia
2,697
Georgia
2,673
Cyprus
1,790
Jordan
1,201

Iraq
1,173
Brunei
429
Syria
379
Australia
15,176
New Zealand
1,041
Why Participate
![]()
● Real-Life Scenarios Make Math More Engaging
Integrating mathematical knowledge into real-world contexts such as shopping, games, and mazes allows students to intuitively experience the fun and practicality of math in familiar situations.
● Rich Graphical Applications Turn Abstraction into Tangibility
Through engaging activities like paper folding, puzzles, and graphic challenges, abstract mathematical concepts are transformed into visual problems, effectively nurturing spatial imagination.
![]()
![]()
● Strategic Thinking Stimulates Mathematical Insight
Encouraging students to think beyond formulaic approaches and employ strategies like logical reasoning and pattern recognition helps cultivate mathematical insight and optimization awareness.
● Scientific Design Nudges Students Forward
Problems are divided into six difficulty levels, precisely tailored to different learning stages. With progressively increasing challenges, students are motivated to tackle difficulties and continuously build a sense of achievement.
![]()
MK Rules and Awards
Rules & Information

- Language: English&Chinese
- Location: Paper-based in partnering school (online service application accepted)
- Format: Individual test, multiple-choice questions
- Participant: Grades 1-12, categorized into six levels
| Level | Grade | Date | Scoring System |
| Level A | Grades 1-2 | Mar. 28, 2026 (Sat.)
9:00-10:15 |
Level A-B: 24 multiple-choice questions with a total score of 120. The starting score is 24 points. Questions 1-8 are worth 3 points. Questions 9-16 are worth 4 points. Questions 17-24 are worth 5 points. (1 point will be deducted for wrong answers, and no point will be deducted for blank answers.) |
| Level B | Grades 3-4 | Mar. 28, 2026 (Sat.)
10:30-11:45 |
|
| Level C | Grades 5-6 | Level C-F: 30 multiple-choice questions with a total score of 150. The starting score is 30 points. Questions 1-10 are worth 3 points. Questions 11-20 are worth 4 points. Questions 21-30 are worth 5 points. (1 point will be deducted for wrong answers, and no point will be deducted for blank answers.) | |
| Level D | Grades 7-8 | Mar. 28, 2026 (Sat.)
14:00-15:15 |
|
| Level E | Grades 9-10 | ||
| Level F | Grades 11-12 |
* Level A provide questions reading to ensure that young participants can understand the questions.
* Students can choose to register for the level higher than their grade, but can not choose the level lower than their grade.
Awards
Global Awards
- Math Kangaroo Perfect Score: Full score
- Top Gold: Top 5%
- Gold Award: Top 15%
National Awards
- Silver Award: Top 30%
- Bronze Award: Top 45%
- Proficiency Award: Top 25% by Province / Municipality / Autonomous Region / Special autonomous region (after national awards)
* Each grade will be awarded separately. Students with a perfect score will receive a medal as well.
Academic Resources

Sample Questions

Math Kangaroo Problem Sample Book & Math Word Book

Past Decade's Exam Papers & Official Solutions

Core topics

Common Mistakes Questions & Solutions Book
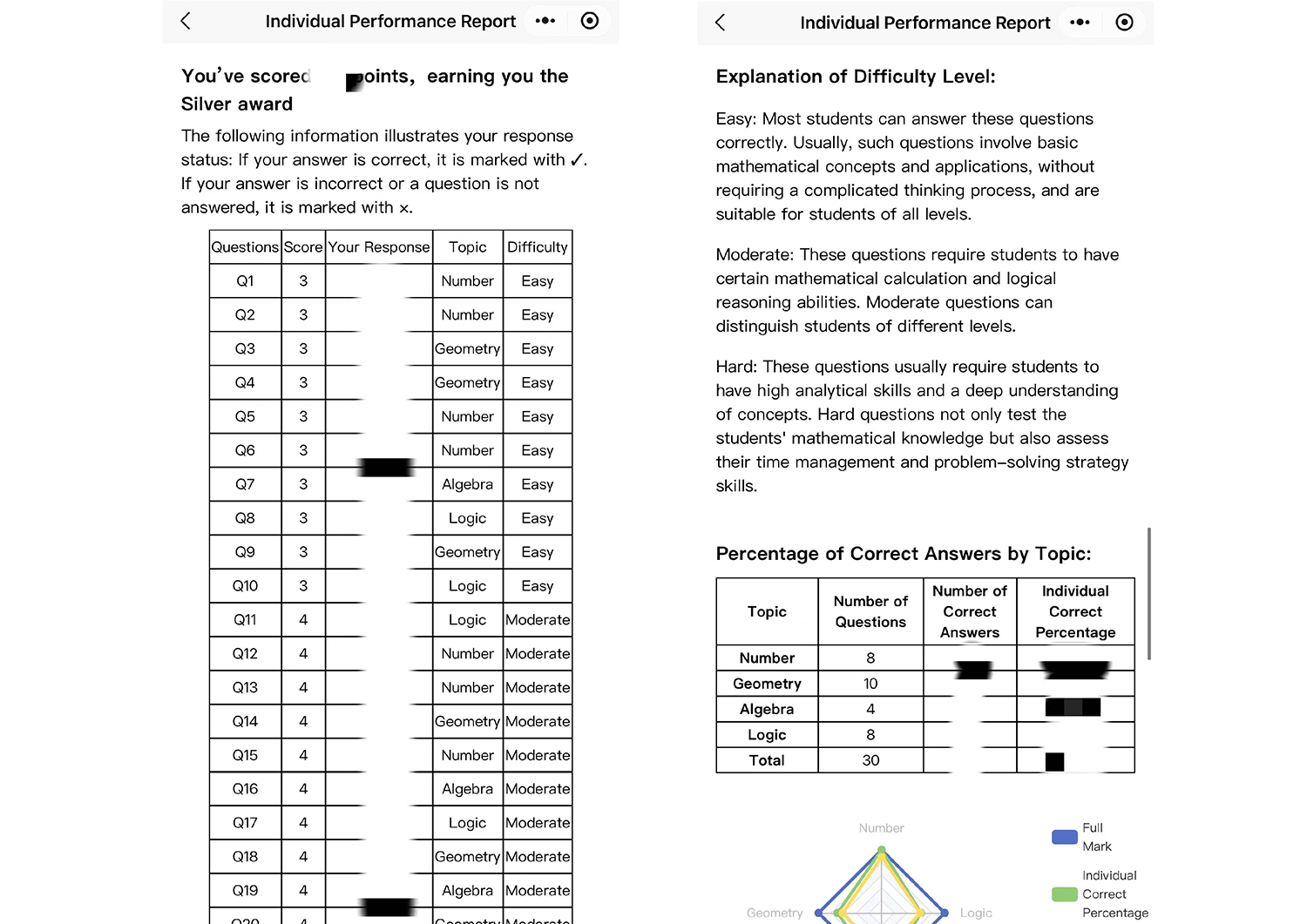
Performance Report (For Individual Students or Schools)

Math Kangaroo Annual Book
If needed, please scroll to the bottom of the webpage to select a teacher and contact them.
Sample Questions
2025 Level A Q5
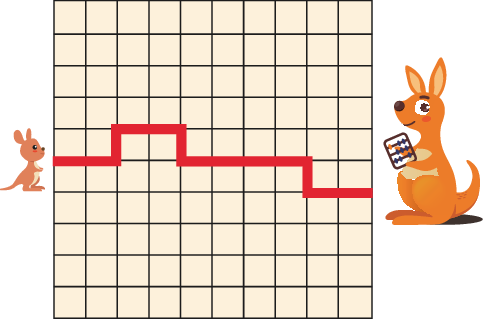
5 baby kangaroos are hopping to their mothers along the paths shown below. Which path is the shortest?
5 只袋鼠宝宝沿着下方所示的路径跳向它们的妈妈。请问哪条路径最短?
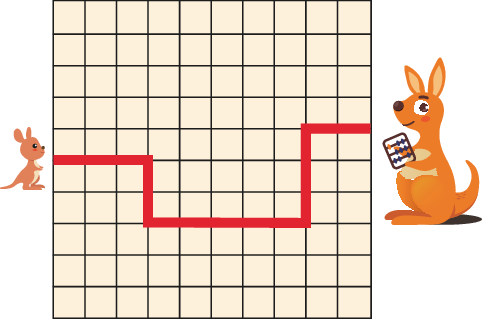
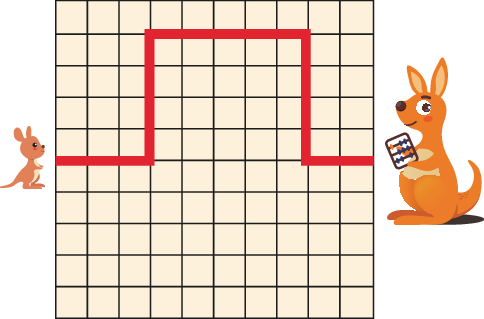
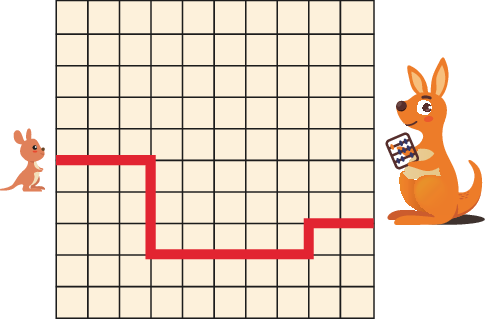
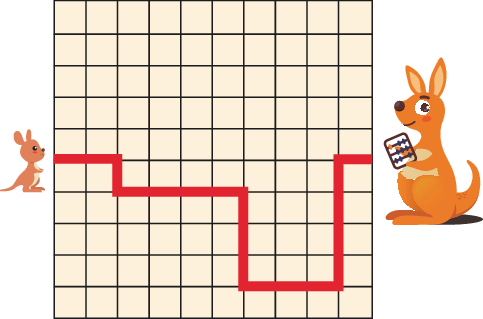
正确答案/Answer:A
Solution: Each path has only horizontal and vertical segments. The total length of the horizontal segments is the same for each path. So it is enough to compare the total length of the vertical segments. Option A has the shortest path.
解析:每条路径仅包含水平与垂直段。水平段总长度相同,因此只需要比较垂直段的总长度。选项 A 的路径最短。
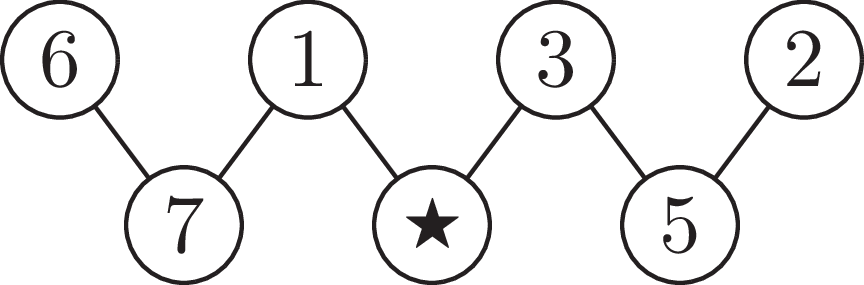
2025 Level B Q15
Maria fills the circles with the numbers 1, 2, 3, 4, 5, 6 and 7. The number in each of the lower circles is equal to the sum of the two numbers in the connected circles above it.
What number is in the circle marked with ![]() ?
?
小玛在圆圈里填入数字 1、2、3、4、5、6 和 7。图片中位于下方的每个圆圈里的数字等于与它相连的上方两个圆圈中的数字之和。请问标有 ![]() 的圆圈里的数字是什么?
的圆圈里的数字是什么?

- (A) 2
- (B) 3
- (C) 4
- (D) 5
- (E) 7
正确答案/Answer:C
Solution: 1, 2, 3, 4, 5, 6, 7 are the numbers to fill in. 6 is already there. Below the 6, the sum should be higher than 6, so that could only be the 7. The 7 is now at the bottom left circle. We have to find the answer for 6 + ... = 7, so, this could only be 1. We now have left 2, 3, 4, 5. The two highest numbers should be sums, so, go in the bottom row. The 4 cannot be formed with summing a pair out of 2, 3, or 5. Therefore, the 4 has to come from 1 + ... = 4. This gives the position of 4 in the bottom middle, which is the correct answer (the star), and the 3 in the top. Then, the 5 is on the bottom right, and 2 on the top right.
解析:1、2、3、4、5、6、7是要填入的数字,其中6已经填好。在6的下方,所填数字之和应大于6,因此只能是7。7现在在左下角的圆圈中。我们需要找到 6 + … =7 的答案,所以只能是1。现在剩下2、3、4、5。两个最大的数字应作为和放在底行。4 无法由2、3或5中的任意两个数字相加得到,因此4必须来自 1 + … =4。这确定了 4是正确答案,填在底行中间的星形位置;3填在顶部;然后5填在底行右侧,2填在顶部右上角。
2025 Level C Q6
Container A holds 8 litres of water. All five plugs at the bottom of container A are taken out at the same time and the water flows out. What volume of water flows into container B?
容器 A 里装有 8 升水,当其底部的五个塞子被同时拔出时,水随即流出。请问流入容器 B 中的水的体积是多少?
- (A) 3 litres 3 升
- (B) 4 litres 4 升
- (C) 5 litres 5 升
- (D) 6 litres 6 升
- (E) 8 litres 8 升
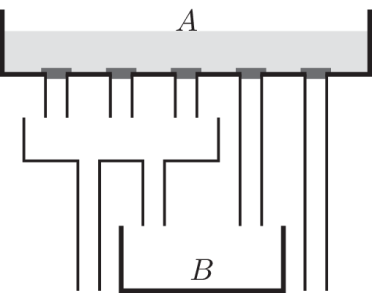
正确答案/Answer:B
Solution:The first 5 plugs get 1.6 L each. The three plugs on the left side have in total 4.8 L. These 4.8 L are divided into two new plug, that is 2.4 L in each. The two plugs on the right have 1.6 L each. So, in container B it will get 2.4 L + 1.6 L = 4 L.
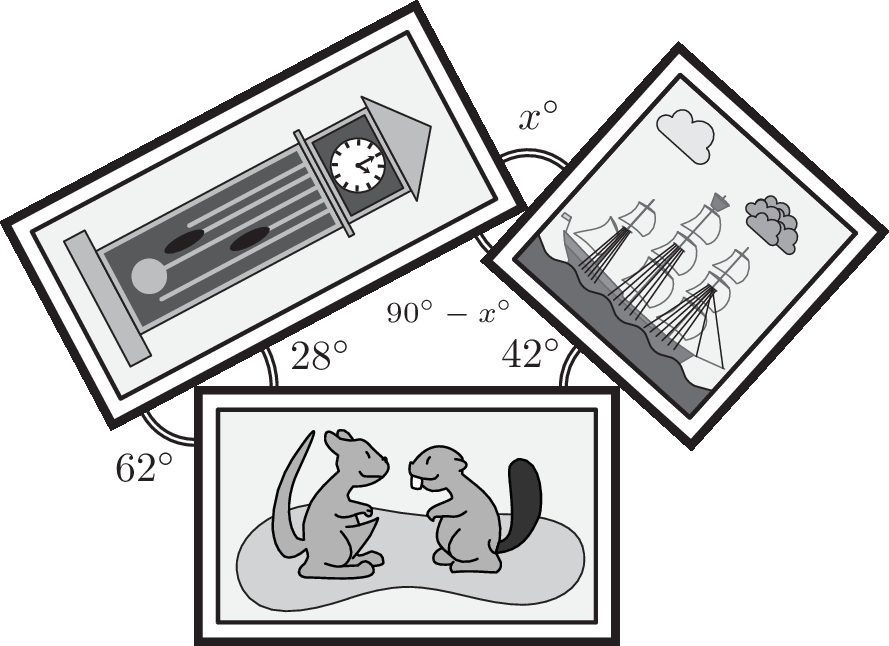
解析:通过前 5 个塞孔各流出 1.6 升 。通过左侧三个塞孔共流出 4.8 升,这些水被均分到两个新塞孔,每个塞孔流出 2.4 升。右侧两个塞孔各流出 1.6升。因此,容器 B 将得到 2.4 升 + 1.6 升 = 4 升。2025 Level D Q14
Louise places three rectangular pictures in the way shown.
What is the value of x?
Louise 把三张矩形图片按如图所示的方式摆放。
请问 x 的值是多少?
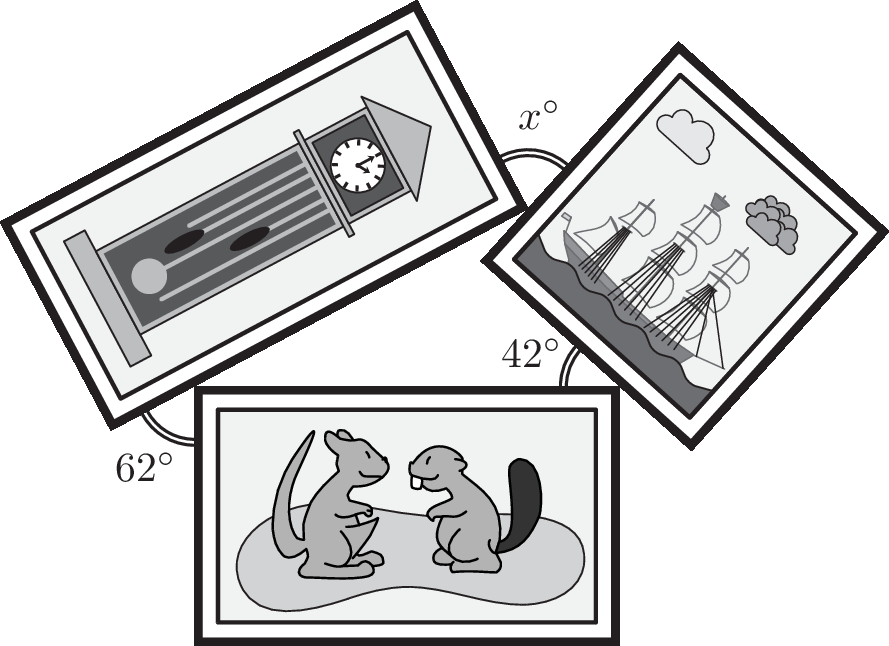
- (A) 64
- (B) 70
- (C) 72
- (D) 76
- (E) 80
正确答案/Answer:B
Solution (解析): 90 − 62 = 28; 28 + 42 + (90 − x) = 180 − 90; x = 70
2025 Level E Q20
Five bricks are placed on the ground, as shown. Peter can only remove a brick if there are no bricks on top of it. He selects one of the available bricks at random and removes it, until all the bricks are removed. What is the probability that the brick numbered 4 is the third brick to be removed?
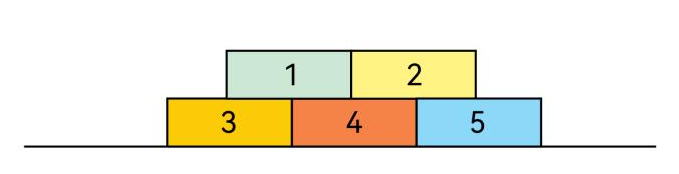
如图所示,地面上放置着五块砖。Peter 只能移除上方没有其他砖块的砖。他每次随机选择一块可以移除的砖块并将其拿走,直到所有砖块都被移除。请问移除的第三块砖是编号为 4 的砖块的概率是多少?
- (A) 1/3
- (B) 1/4
- (C) 1/5
- (D) 1/6
- (E)1/8
正确答案/Answer:D
Solution:To remove the brick N4 we need to remove the first row of bricks (N1 and N2). So we’ll need 3 moves.
Case 1. We remove brick N1( Probability P=1/2). Then N2 will have to go ( P=1/2 ). To have N4 removed we have a chance of P=1/3. So the probability for this case is 1/2 · 1/2 · 1/3 = 1/12.
Case 2. Because of the symmetry the same happens if we remove brick N2 first. Since the events are exclusive the answer is 1/12 + 1/12 = 1/6 .
解析:为了移除砖块 N4,我们需要先移除第一行的砖块(N1 和 N2)。因此,我们需要 3 步。
情况 1 :我们移除砖块N1 ( 概率 P=1/2 )。那么 N2 将不得不被移除( P=1/2 )。为了移除 N4,我们有 P=1/3 的机会。因此,这种情况的概率是 1/2 · 1/2 · 1/3 = 1/12。
情况 2 :由于对称性,如果我们先移除砖块 N2,后续情况相同。
由于这些事件是互斥的,所以答案是 1/12 + 1/12 = 1/6。
2025 Level F Q16
On a 4 × 4 giant chessboard there are 16 kangaroos, one in each square. On each turn, each of the kangaroos jumps to a neighbouring square (up, down, left or right, but not diagonally). All kangaroos stay on the board. There can be several kangaroos on any square. After 100 turns, what is the largest possible number of empty squares?

在一个 4 × 4 的巨型棋盘上,共有 16 只袋鼠,每个格子中各有一只。在每一回合中,每只袋鼠都会跳向相邻的格子(可以向上、向下、向左或向右,但不能对角线跳跃)。所有袋鼠始终留在棋盘上,且每个格子里可以容纳多只袋鼠。请问经过 100 回合后,棋盘上最多可能有多少个空格子?
- (A) 15
- (B) 14
- (C) 12
- (D) 10
- (E) 8
正确答案/Answer:B
Solution: Each kangaroo changes the color of their square each turn. Since they start on two different colors, there must be at least two squares with kangaroos after each turn, so at most 14 squares can be empty. 14 empty squares is possible: for example all the kangaroos from black squares can go to the bottom left corner and all the kangaroos from white squares to the bottom right corner. This is possible since the number of jumps is even.
解析:每只袋鼠每回合都会改变其所在格子的颜色。由于它们起始于两种不同颜色的格子,每回合后至少有两个格子有袋鼠,所以最多可以有 14 个空格子。14 个空格子是可能的:例如,所有来自黑色格子的袋鼠都跳到左下角,所有来自白色格子的袋鼠都跳到右下角。由于跳跃次数是偶数,这是可以实现的。
MK Tournament rules and awards
Rules&Information
Language: English and Chinese
Date:
- Paper-based Exam (in partnering schools)
Levels A&B&C&D&E&F: Dec. 1st - 5th, 2025
- Online Exam (Team must sit at one location)
Levels A&B: Dec. 6th (Sat), 2025, 10:00-10:45
Levels C&D&E&F: Dec. 6th (Sat), 2025, 10:00-11:00
* To take the paper-based exam, please coordinate with your school teacher to apply for partnering school.
Difficulty Level: Grade 1-12, categorized into six levels
- Level A: Grade 1-2
- Level B: Grade 3-4
- Level C: Grade 5-6
- Level D: Grade 7-8
- Level E: Grade 9-10
- Level F: Grade 11-12
* Level A provide questions reading to ensure that young participants can understand the questions.
* Students may register for a higher level (but not a lower one) than their current grade.
Team Formation Rules (By Level)
- Level A-B: Teams of 2 students
- Level C-F: Teams of 2-3 students
* Team members must all be at the same Difficulty Level. Cross-level teams are not permitted.
Assessment Scope: Based on the official problem- setting approach of the Math Kangaroo, the challenge evaluates four key dimensions: Geometry, Algebra, Number, Logic
Format: Within 45-60 minutes, team members must communicate and collaborate to complete a set of questions, submitting only one answer sheet per team.
Awards (Each Level will be awarded separately)
- Top Gold: Top 10% of teams
- Gold Award: Top 30% of teams
- Silver Award: Top 40% of teams
- Bronze Award: Top 60% of teams
- Excellence Award: Top 85% of teams
* Gold Award winners and above will be invited to the annual Math Kangaroo Asia Championship held every summer in Boao, Hainan.
| Level | Duration | Question Types & Scorin |
| Level A, B | 45min | Questions 1-20: Multiple-choice (4 points each), Questions 21-24: Fill-in-the-blank (5 points each). Total score: 100 points. No points deducted for incorrect answer. |
| Level C, D, E, F | 60min | Questions 1-25: Multiple-choice (4 points each), Questions 26-30: Fill-in-the-blank (5 points each). Total score: 125 points. No points deducted for incorrect answer. |
 Math Kangaroo Asia Championship
Math Kangaroo Asia Championship
To deepen the dissemination of the "Kangaroo Without Borders", with the goal of nurturing future mathematicians, Kangaroo Global organizes the International Math Camp every summer. It exclusively invites award winners, primarily those with gold or above awards. The content of the camp is consistent across continents, with slight adjustments
based on the host country's resources.
In 2026, the Math Kangaroo Asia Championship will bring together gold medalists of the Math Kangaroo from various countries and regions, including China (with Hong Kong, Macao, and Taiwan), the United States, Ghana, Myanmar, Turkey, Saudi Arabia, Malaysia, Vietnam, Thailand, Singapore, South Korea, India, and Kazakhstan. Guided by internationally renowned Mathematics experts, students will delve into advanced mathematical topics, compete and interact with peers from across the globe, and partake in a vibrant celebration of Mathematical thinking!
Math Kangaroo China Academic Board
Math Kangaroo China Academic Board Invitation
Dear Teachers,
Since 2019, ASEEDER has been collaborating with the Math Kangaroo Global Organizing Committee to introduce Math Kangaroo to China. Math Kangaroo is one of the world's largest mathematics activity for young minds, engaging over 6.5 million students from 109 countries in 2025. Unlike traditional mathematics assessments that emphasize high difficulty and challenges, Math Kangaroo aims to stimulate children's interest and confidence in learning mathematics through engaging and life-relevant problems. It cultivates students' mathematical thinking and enhances their skills in reading, comprehension, analysis, and problem-solving, making it suitable for students of all grades and mathematical proficiency levels.
"Kangaroo Without Borders"—one of its most significant initiatives involves designing the annual Math Kangaroo problems. Targeting students from grades 1 to 12, all problems are in multiple-choice format. Each year, Math Kangaroo's national organizing committees from member countries invite expert teams to submit local problems, which are then reviewed and selected by the global committee to form the official problem sets for all levels worldwide. This inclusive approach to problem selection ensures diversity, flexibility, and fun, contributing to the unique appeal and vitality of Math Kangaroo.
Additionally, the Math Kangaroo China Academic Board holds annual seminars to discuss and develop mathematics teaching methodologies. Furthermore, the official list of all members is published each year on the Chinese regional official website. Therefore, we sincerely welcome interested applicants from your school to join the Math Kangaroo China Academic Board!
Math Kangaroo China
ASEEDER
Math Kangaroo China Support Program for Rural Schools
Echoing Math Kangaroo's mission of expanding the world's math population through unique challenges, Math Kangaroo China committee is launching its rural support program. Any rural public school in China can apply to participate in Math Kangaroo free of charge.
Please contact math@seedasdan.org to request for the application form or for further information.
FAQ
If, for some reason, the student is unable to attend after paying the fee, please contact us. If you apply before the registration deadline, 25% of the registration fee will be deducted as academic materials and service fees. If you apply after the registration deadline, no refund will be given.