46 年历史
等级A 提供读题功能
袋鼠波兰营和袋鼠亚洲营
简介
 袋鼠数学思维趣味活动 由澳大利亚著名数学家Peter O'Halloran 于1980 年发起。1991 年,法国两位著名数学教育家成立正式组委会并在欧洲推广该活动,为了向Peter O'Halloran 致敬,将该活动正式取名为“袋鼠数学思维趣味活动”,全球组委会总部位于法国巴黎。不同于传统数学测评强调的高难度和挑战性,袋鼠数学思维趣味活动的宗旨是用有趣生动、接近生活的题目,激发孩子们数学学习兴趣及自信,培养学生数学思维,训练学生阅读、理解、分析和解决问题的能力,适合各年级各种数学水平同学参加。袋鼠数学思维趣味活动逐步风靡世界,成为全球极具规模的青少年国际数学思维趣味活动。截止目前,全球有109 个国家和地区承办此活动,2025 年,全球约650 万学生参与其中。
袋鼠数学思维趣味活动 由澳大利亚著名数学家Peter O'Halloran 于1980 年发起。1991 年,法国两位著名数学教育家成立正式组委会并在欧洲推广该活动,为了向Peter O'Halloran 致敬,将该活动正式取名为“袋鼠数学思维趣味活动”,全球组委会总部位于法国巴黎。不同于传统数学测评强调的高难度和挑战性,袋鼠数学思维趣味活动的宗旨是用有趣生动、接近生活的题目,激发孩子们数学学习兴趣及自信,培养学生数学思维,训练学生阅读、理解、分析和解决问题的能力,适合各年级各种数学水平同学参加。袋鼠数学思维趣味活动逐步风靡世界,成为全球极具规模的青少年国际数学思维趣味活动。截止目前,全球有109 个国家和地区承办此活动,2025 年,全球约650 万学生参与其中。
2024 年,在十七个国家和地区联合倡导下,袋鼠数学全球组委会开始在全球推广“袋鼠数学团体趣味挑战”,旨在提供更多元有趣的数学学习方式,让同学们通过数学产生链接,共同解决问题。同学们在团队合作的同时,激发数学学习兴趣,感受数学魅力。
为促进全球数学精英学子的交流,深化“袋鼠数学无国界”理念的传播,以培养未来的数学家为目标,袋鼠全球每年暑期都举办袋鼠国际数学营,专邀荣获奖项(主要以金奖及以上奖项为主)的选手参与。各大洲的袋鼠国际数学营内容模块基本一致,根据主办国的数学资源进行微调。
袋鼠数学晋级体系
2025年,全球约650万学生参加了“袋鼠数学思维趣味活动”
 美国
美国
53,562 墨西哥
墨西哥
34,406 洪都拉斯
洪都拉斯
19,879 哥斯达黎加
哥斯达黎加
7,578 加拿大
加拿大
6,875 多米尼加共和国
多米尼加共和国
5,295 牙买加
牙买加
4,680 波多黎各
波多黎各
2,216
 巴西
巴西
1,502,507 秘鲁
秘鲁
36,442 哥伦比亚
哥伦比亚
35,027 委内瑞拉
委内瑞拉
18,071 阿根廷
阿根廷
14,708 玻利维亚
玻利维亚
11,988 智利
智利
5,443 巴拉圭
巴拉圭
3,351
 厄瓜多尔
厄瓜多尔
1,970 巴拿马
巴拿马
1,594 乌拉圭
乌拉圭
521 德国
德国
881,500 捷克共和国
捷克共和国
420,653 法国
法国
311,700 波兰
波兰
304,635 俄罗斯
俄罗斯
248,920
 加泰罗尼亚
加泰罗尼亚
148,672 奥地利
奥地利
127,169 比利时
比利时
121,315 荷兰
荷兰
109,878 瑞典
瑞典
101,402 白俄罗斯
白俄罗斯
87,058 斯洛伐克
斯洛伐克
75,982 葡萄牙
葡萄牙
72,522
 斯洛文尼亚
斯洛文尼亚
70,281
意大利
66,925 乌克兰
乌克兰
62,384 瑞士
瑞士
62,157 保加利亚
保加利亚
58,019 匈牙利
匈牙利
36,563 克罗地亚
克罗地亚
34,494 立陶宛
立陶宛
31,358
 西班牙
西班牙
26,589 爱沙尼亚
爱沙尼亚
22,916 罗马尼亚
罗马尼亚
20,933 芬兰
芬兰
20,922 挪威
挪威
15,315 英国
英国
13,320 丹麦
丹麦
13,221 拉脱维亚
拉脱维亚
12,891

塞尔维亚
11,429 摩尔多瓦
摩尔多瓦
9,190 北马其顿
北马其顿
7,472 波斯尼亚和黑塞哥维那
波斯尼亚和黑塞哥维那
5,191 黑山共和国
黑山共和国
3,288 科索沃
科索沃
2,015 阿尔巴尼亚
阿尔巴尼亚
1,399 爱尔兰
爱尔兰
799
 摩洛哥
摩洛哥
85,882 埃及
埃及
25,650 加纳
加纳
8,493 南非
南非
7,435 喀麦隆
喀麦隆
3,318 乌干达
乌干达
2,913 博茨瓦纳
博茨瓦纳
1,587 卢旺达
卢旺达
1,576
 尼日利亚
尼日利亚
1,176 肯尼亚
肯尼亚
600 毛里塔尼亚
毛里塔尼亚
420 赞比亚
赞比亚
340 突尼斯
突尼斯
201 马里共和国
马里共和国
172 印度尼西亚
印度尼西亚
143,720 哈萨克斯坦
哈萨克斯坦
111,689
 印度
印度
80,404 马来西亚
马来西亚
76,949 土耳其
土耳其
420 巴基斯坦
巴基斯坦
46,192 沙特阿拉伯
沙特阿拉伯
42,109 菲律宾
菲律宾
35,398 越南
越南
27,843 以色列
以色列
17,481
 蒙古
蒙古
14,289 乌兹别克斯坦
乌兹别克斯坦
13,557 吉尔吉斯斯坦
吉尔吉斯斯坦
11,720 韩国
韩国
11,050
伊朗
11,023 阿富汗
阿富汗
9,896 泰国
泰国
6,230 新加坡
新加坡
6,106
 巴勒斯坦
巴勒斯坦
5,161 缅甸
缅甸
3,977 黎巴嫩
黎巴嫩
3,200 卡塔尔
卡塔尔
3,164 亚美尼亚
亚美尼亚
2,697 格鲁吉亚
格鲁吉亚
2,673 塞浦路斯
塞浦路斯
1,790 约旦
约旦
1,201
 伊拉克
伊拉克
1,173 文莱
文莱
429 叙利亚
叙利亚
379 澳大利亚
澳大利亚
15,176 新西兰
新西兰
1,041
为什么参与
![]()
● 生活化情景,让数学更有趣
将数学知识融入购物、游戏、迷宫等真实场景,让学生在熟悉的情境中直观感受数学的趣味与实用。
● 丰富的图形运用,化抽象为具体
通过折纸、拼图、图形迷阵等趣味形式,将抽象数学概念转化为可视化的题目,有效培养空间想象力。
![]()
![]()
● 策略性思考,激发数学洞察力
鼓励跳出公式套路,运用逻辑推理、模式识别等策略解决问题,从而培养数学洞察力与优化意识。
● 科学的机制设计,鼓励积极挑战
题目分为6个难度等级,精准匹配不同学段能力。难度循序渐进,激励学生勇闯难关,持续积累成就感。
![]()
满分学生分享

— 王同学

— 班同学

— 刘同学

— 姚同学
规则与奖项
规则

- 语言:中英文双语
- 地点:全国各教学合作学校校内(学校申请可提供在线测评服务)
- 形式:个人,选择题
- 参与年级:1-12 年级(小学一年级至高三年级),分为六个难度等级
| 等级 | 对应年级 | 时间 | 评分标准 |
| 等级 A | 1-2 年级(小学) | 2026 年 3 月 28 日(周六) 9:00-10:15(75 分钟) |
等级A-B:共 24 道选择题,总分 120 分,起始分数为 24 分,1-8 题每题 3 分,9-16 题每题 4 分,17-24 题每题 5 分,答错扣 1 分,不答不扣分 |
| 等级 B | 3-4 年级(小学) | 2026 年 3 月 28 日(周六)
10:30-11:45(75分钟) |
|
| 等级 C | 5-6 年级(小学) | 等级C-F:共 30 道选择题,总分 150 分,起始分数为 30 分,1-10 题每题 3 分,11-20 题每题 4 分,21-30 题每题 5 分,答错扣 1 分,不答不扣分 | |
| 等级 D | 7-8 年级(初一、初二) | 2026 年 3 月 28 日(周六) 14:00-15:15(75 分钟) |
|
| 等级 E | 9-10 年级(初三、高一) | ||
| 等级 F | 11-12 年级(高二、高三) |
* 等级A 测评提供读题功能,确保小选手都能听懂题目
* 学生可以选择报名高于所在年级的级别考试,但不允许选择低于所在年级的级别
* 查看对应年级时,不同地区和课程体系学制或有不同,请以年级为准
奖项设置
全球奖项
- Math Kangaroo成就奖:满分同学将获该奖项
中国区奖项
- 超级金奖 Top Gold:排名前 5%
- 金奖 Gold Award:排名前 15%
- 银奖 Silver Award:排名前 30%
- 铜奖 Bronze Award:排名前 45%
- 数学技能奖 Proficiency Award:各省 /直辖市 /自治区/ 特别行政区(除全国奖项之外)前 25%
* 每个年级单独评奖,满分奖的同学也将同时获得奖牌

参与证书

获奖证书

满分奖牌
1. 倒计时结束后系统自动跳转APASS登录页,请按照提示登录系统
2. 登录后免费领取APASS7天试用会员,即可在线进行袋鼠真题演练哦
学术资料

样题练习

袋鼠数学精彩题目集锦

近十年真题与官方解析

考察知识点

袋鼠数学易错题集锦
成绩报告(针对个人/学校)

袋鼠数学单词手册
如有需要,请划至网页最下方添加对应年级的顾问老师获取。
2026年袋鼠数学年刊
——洞察趋势、连接全球的年度窗口
本刊完整记载2025年度袋鼠活动全景,各等级测评大纲,并独家收录师生感言、全球征题标准与专家命题心法,是一本集年度总结、学术参考与灵感启发于一体的必备指南

袋鼠数学动画片-Kanga奇妙探险之旅
第一集——《神龟背上的秘密》
让我们跟随勇敢的小袋鼠Kanga和聪明的蜂博士,前往四千年前的中国东方,开启一段用数学知识战胜混乱怪的奇妙旅程!
样题
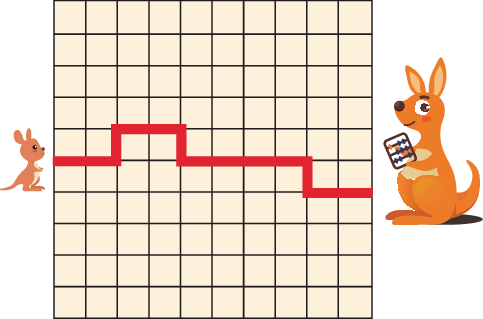
2025 Level A Q5
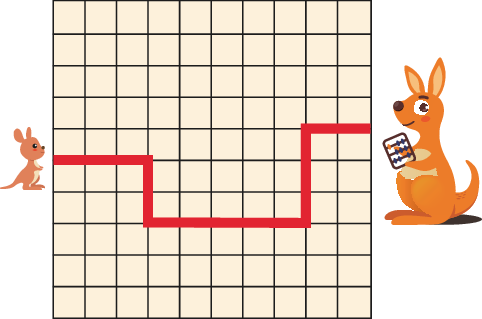
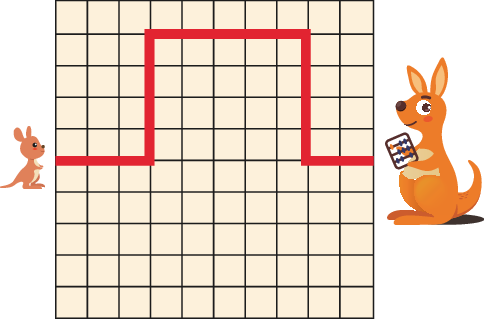
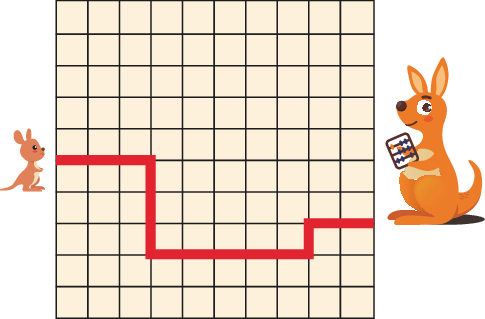
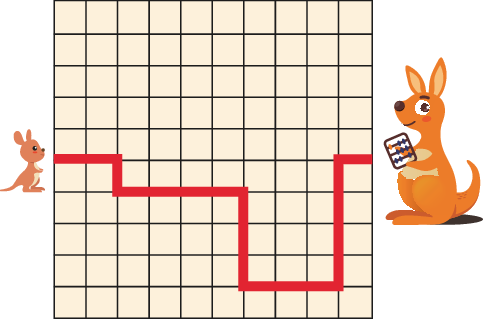
5 baby kangaroos are hopping to their mothers along the paths shown below. Which path is the shortest?
5 只袋鼠宝宝沿着下方所示的路径跳向它们的妈妈。请问哪条路径最短?
(A)
(B)
(C)
(D)
(E)
正确答案/Answer:A
Solution: Each path has only horizontal and vertical segments. The total length of the horizontal segments is the same for each path. So it is enough to compare the total length of the vertical segments. Option A has the shortest path.
解析:每条路径仅包含水平与垂直段。水平段总长度相同,因此只需要比较垂直段的总长度。选项 A 的路径最短。
2025 Level B Q15
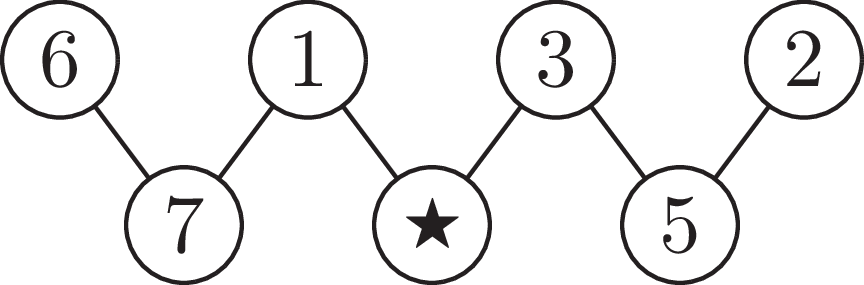
Maria fills the circles with the numbers 1, 2, 3, 4, 5, 6 and 7. The number in each of the lower circles is equal to the sum of the two numbers in the connected circles above it.
What number is in the circle marked with ![]() ?
?
小玛在圆圈里填入数字 1、2、3、4、5、6 和 7。图片中位于下方的每个圆圈里的数字等于与它相连的上方两个圆圈中的数字之和。请问标有 ![]() 的圆圈里的数字是什么?
的圆圈里的数字是什么?

- (A) 2
- (B) 3
- (C) 4
- (D) 5
- (E) 7
正确答案/Answer:C
Solution: 1, 2, 3, 4, 5, 6, 7 are the numbers to fill in. 6 is already there. Below the 6, the sum should be higher than 6, so that could only be the 7. The 7 is now at the bottom left circle. We have to find the answer for 6 + ... = 7, so, this could only be 1. We now have left 2, 3, 4, 5. The two highest numbers should be sums, so, go in the bottom row. The 4 cannot be formed with summing a pair out of 2, 3, or 5. Therefore, the 4 has to come from 1 + ... = 4. This gives the position of 4 in the bottom middle, which is the correct answer (the star), and the 3 in the top. Then, the 5 is on the bottom right, and 2 on the top right.
解析:1、2、3、4、5、6、7是要填入的数字,其中6已经填好。在6的下方,所填数字之和应大于6,因此只能是7。7现在在左下角的圆圈中。我们需要找到 6 + … =7 的答案,所以只能是1。现在剩下2、3、4、5。两个最大的数字应作为和放在底行。4 无法由2、3或5中的任意两个数字相加得到,因此4必须来自 1 + … =4。这确定了 4是正确答案,填在底行中间的星形位置;3填在顶部;然后5填在底行右侧,2填在顶部右上角。
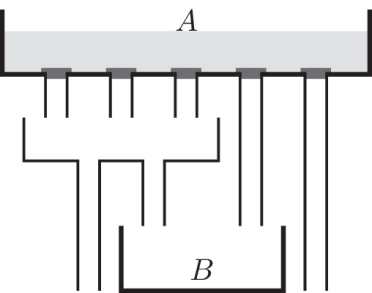
2025 Level C Q6
Container A holds 8 litres of water. All five plugs at the bottom of container A are taken out at the same time and the water flows out. What volume of water flows into container B?
容器 A 里装有 8 升水,当其底部的五个塞子被同时拔出时,水随即流出。请问流入容器 B 中的水的体积是多少?
- (A) 3 litres 3 升
- (B) 4 litres 4 升
- (C) 5 litres 5 升
- (D) 6 litres 6 升
- (E) 8 litres 8 升
正确答案/Answer:B
Solution:The first 5 plugs get 1.6 L each. The three plugs on the left side have in total 4.8 L. These 4.8 L are divided into two new plug, that is 2.4 L in each. The two plugs on the right have 1.6 L each. So, in container B it will get 2.4 L + 1.6 L = 4 L.
解析:通过前 5 个塞孔各流出 1.6 升 。通过左侧三个塞孔共流出 4.8 升,这些水被均分到两个新塞孔,每个塞孔流出 2.4 升。右侧两个塞孔各流出 1.6升。因此,容器 B 将得到 2.4 升 + 1.6 升 = 4 升。
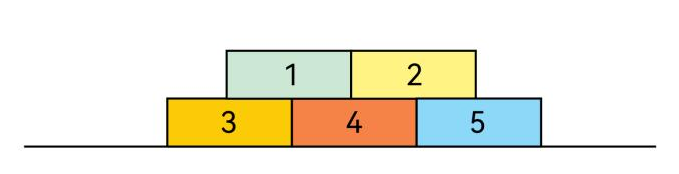
2025 Level D Q14
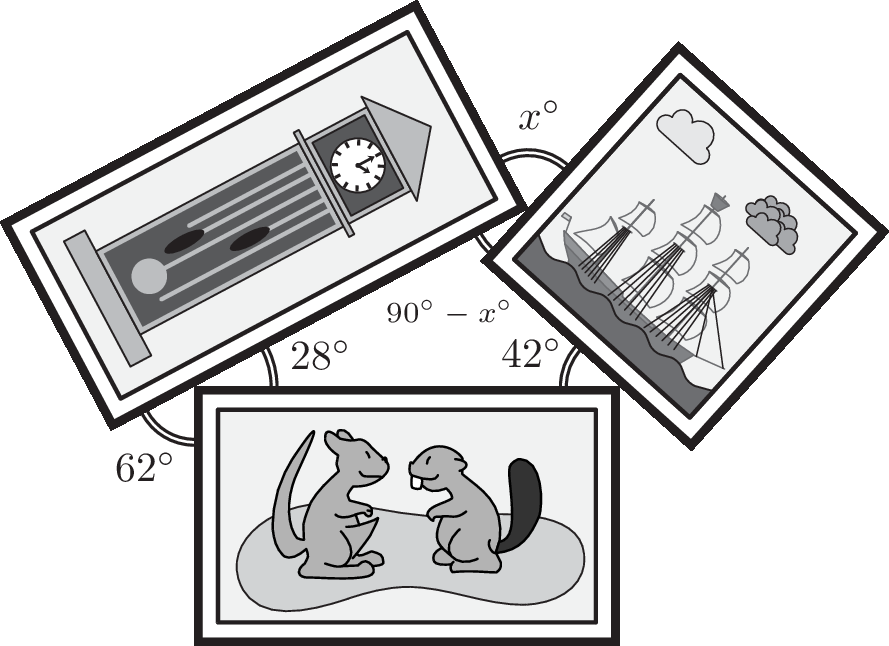
Louise places three rectangular pictures in the way shown. What is the value of x?
Louise 把三张矩形图片按如图所示的方式摆放。 请问 x 的值是多少?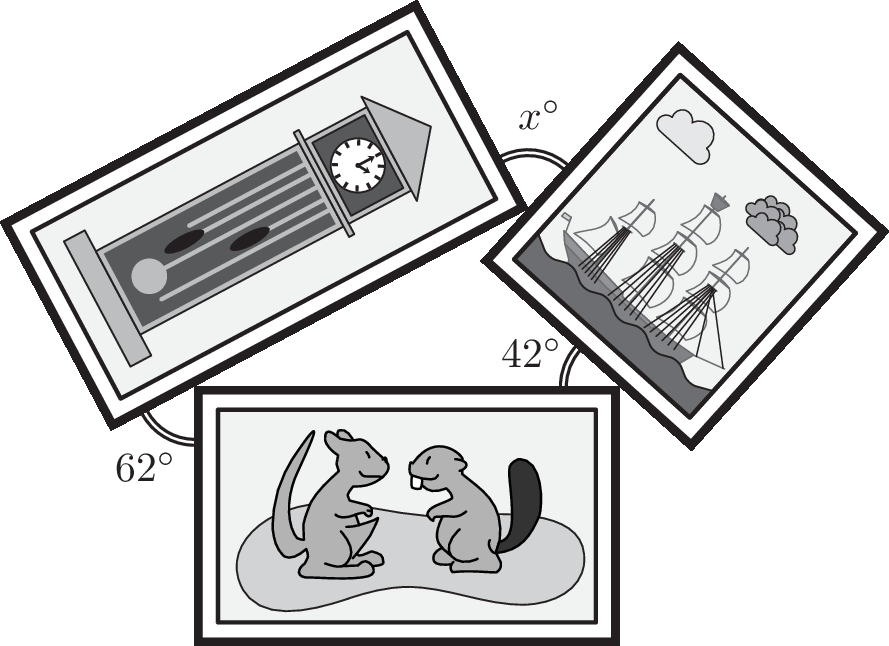
- (A) 64
- (B) 70
- (C) 72
- (D) 76
- (E) 80
正确答案/Answer:B
Solution (解析): 90 − 62 = 28; 28 + 42 + (90 − x) = 180 − 90; x = 70
2025 Level E Q20
Five bricks are placed on the ground, as shown. Peter can only remove a brick if there are no bricks on top of it. He selects one of the available bricks at random and removes it, until all the bricks are removed. What is the probability that the brick numbered 4 is the third brick to be removed?
如图所示,地面上放置着五块砖。Peter 只能移除上方没有其他砖块的砖。他每次随机选择一块可以移除的砖块并将其拿走,直到所有砖块都被移除。请问移除的第三块砖是编号为 4 的砖块的概率是多少?
- (A) 1/3
- (B) 1/4
- (C) 1/5
- (D) 1/6
- (E)1/8
正确答案/Answer:D
Solution:To remove the brick N4 we need to remove the first row of bricks (N1 and N2). So we’ll need 3 moves.
Case 1. We remove brick N1( Probability P=1/2). Then N2 will have to go ( P=1/2 ). To have N4 removed we have a chance of P=1/3. So the probability for this case is 1/2 · 1/2 · 1/3 = 1/12.
Case 2. Because of the symmetry the same happens if we remove brick N2 first. Since the events are exclusive the answer is 1/12 + 1/12 = 1/6 .
解析:为了移除砖块 N4,我们需要先移除第一行的砖块(N1 和 N2)。因此,我们需要 3 步。
情况 1 :我们移除砖块N1 ( 概率 P=1/2 )。那么 N2 将不得不被移除( P=1/2 )。为了移除 N4,我们有 P=1/3 的机会。因此,这种情况的概率是 1/2 · 1/2 · 1/3 = 1/12。 情况 2 :由于对称性,如果我们先移除砖块 N2,后续情况相同。 由于这些事件是互斥的,所以答案是 1/12 + 1/12 = 1/6。2025 Level F Q16
On a 4 × 4 giant chessboard there are 16 kangaroos, one in each square. On each turn, each of the kangaroos jumps to a neighbouring square (up, down, left or right, but not diagonally). All kangaroos stay on the board. There can be several kangaroos on any square. After 100 turns, what is the largest possible number of empty squares?

在一个 4 × 4 的巨型棋盘上,共有 16 只袋鼠,每个格子中各有一只。在每一回合中,每只袋鼠都会跳向相邻的格子(可以向上、向下、向左或向右,但不能对角线跳跃)。所有袋鼠始终留在棋盘上,且每个格子里可以容纳多只袋鼠。请问经过 100 回合后,棋盘上最多可能有多少个空格子?
- (A) 15
- (B) 14
- (C) 12
- (D) 10
- (E) 8
正确答案/Answer:B
Solution: Each kangaroo changes the color of their square each turn. Since they start on two different colors, there must be at least two squares with kangaroos after each turn, so at most 14 squares can be empty. 14 empty squares is possible: for example all the kangaroos from black squares can go to the bottom left corner and all the kangaroos from white squares to the bottom right corner. This is possible since the number of jumps is even.
解析:每只袋鼠每回合都会改变其所在格子的颜色。由于它们起始于两种不同颜色的格子,每回合后至少有两个格子有袋鼠,所以最多可以有 14 个空格子。14 个空格子是可能的:例如,所有来自黑色格子的袋鼠都跳到左下角,所有来自白色格子的袋鼠都跳到右下角。由于跳跃次数是偶数,这是可以实现的。
袋鼠数学团体趣味挑战规则
规则
语言:中英文
时间 & 地点:
线下纸考(全国各教学合作学校校内)
● A/B 等级:12 月 1 日 - 12 月 5 日 学校任选 45 分钟进行
● C/D/E/F 等级:12 月 1 日 - 12 月 5 日 学校任选 60 分钟进行
在线考试(由团队成员统一约定场所)
● A/B 等级:12 月 6 日(周六) 10:00-10:45
● C/D/E/F 等级:12 月 6 日(周六) 10:00-11:00
难度等级:面向 1-12 年级学生,共分为 6 个难度等级
- 等级 A:1-2 年级
- 等级 B:3-4 年级
- 等级 C:5-6 年级
- 等级 D:7-8 年级
- 等级 E:9-10 年级
- 等级 F:11-12 年级
* 等级 A 测评提供读题功能,确保小选手都能听懂题目
* 学生可以选择报名高于所在年级的等级考试,但不允许选择低于所在年级的等级考试
组队规则(同等级组队)
- 等级 A-B,2 人组队
- 等级 C-F,2-3 人组队
* 同等级的学生可以自由组队,不允许跨等级组队
考察范围:基于袋鼠数学思维趣味活动官方出题思路,考察四个维度知识运用能力:空间几何、代数函数、数与数论、逻辑推理 (Geometry, Algebra, Number, Logic)
形式:在 45 或 60 分钟内,团队成员之间通过沟通讨论,完成一套团体挑战试卷,每个团队只提交一份答案
奖项设置
- 超级金奖:团队排名前 10%
- 金奖:团队排名前 30%
- 银奖:团队排名前 40%
- 铜奖:团队排名前 60%
- 优秀奖:团队排名前 85%
*每个等级单独评奖
*金奖及以上选手,将有机会获邀参与每年暑期在海南博鳌举办的袋鼠数学亚洲营
| 等级 | 挑战时长 | 题型及分值 |
| 等级 A, B | 45 分钟 | 共 24 道题,1-20 题为选择题,每题 4 分;21-24 题为填空题,每题 5 分,满分 100 分,答错或不答得 0 分 |
| 等级 C, D, E, F | 60 分钟 | 共 30 道题,1-25 题为选择题,每题 4 分,26-30 题为填空题,每题 5 分,满分 125 分,答错或不答得 0 分 |
 袋鼠亚洲营
袋鼠亚洲营
为促进全球数学精英学子的交流,深化“袋鼠数学无国界”理念的传播,以培养未来的数学家为目标,袋鼠全球每年暑期都举办袋鼠国际数学营,专邀荣获奖项(主要以金奖及以上奖项为主)的选手参与。各大洲的袋鼠国际数学营内容模块基本一致,根据主办国的数学资源进行微调。
2026 年袋鼠数学亚洲营计划邀请来自中国(含港澳台地区)、美国、瑞典、加纳、缅甸、土耳其、沙特阿拉伯、马来西亚、越南、泰国、新加坡、韩国、印度、哈萨克斯坦等多国的袋鼠数学金牌选手参加。同学们将在国际知名数学专家的指导下,进行数学主题的深度探讨,并与全球选手同台竞技、交流互动,共享数学思维的盛宴!
袋鼠数学中国专家委员会
袋鼠数学中国专家委员会邀请函
亲爱的老师们:
自2019年起,阿思丹香港(ASEEDER)与袋鼠数学全球组委会合作,将袋鼠数学引入中国。袋鼠数学是全球最大规模的青少年数学思维趣味活动,2025年有来自109个国家的650万左右学生参与。不同于传统数学测评强调的高难度和挑战性,袋鼠数学思维趣味活动的宗旨是用有趣生动、接近生活的题目,激发孩子们数学学习兴趣及自信,培养学生数学思维,训练学生阅读、理解、分析和解决问题的能力,适合各年级各种数学水平同学参加。
“袋鼠无国界”,其最重要的一个活动环节就是设计每一年的袋鼠数学题目。袋鼠数学面对1-12年级的学生,题目全部为选择题。一直以来,袋鼠数学由各成员国组委会邀请专家团队征集本国题目,报送全球组委会进行甄选,最终形成全球各级别真题。这种海纳百川的选题方式,决定了题目的多样性、灵活性、趣味性,也构成了袋鼠数学独特的魅力和生命力。
另外,袋鼠数学中国委员会每年都会举办研讨会,讨论和开发数学教学理念。并且,每年所有的正式成员名单都会在中国区官方网站上公布。因此,我们诚挚欢迎贵校有兴趣的申请者加入袋鼠数学中国专家委员会!
袋鼠数学中国专家委员会
阿思丹香港(ASEEDER)
袋鼠数学乡村支持计划
为响应袋鼠数学通过独特挑战拓展全球数学爱好者群体的使命,袋鼠数学中国委员会现推出乡村支持计划。中国任何一所乡村公立学校都可以申请免费参加袋鼠数学活动。
请通过math@seedasdan.org联系以获取申请表或进一步信息。
常见问题
同学报名缴费之后,因故无法参加课程,请及时联系我们。在报名截止日之前申请,将扣除报名费的25%作为学术材料费及服务费;报名截止日之后申请,将不予退费。